………..Welcome!
In this two page website you will find a way to understand and visualize how planets orbit using methods that are easy to understand. The stepwise combination of gentle math and logic is an approach that is more easily understood compared to the rigorous math that is found in standard textbooks of orbital mechanics. If you are a high school student or teacher or college student or professor or are just a curious learner, you will likely discover that Orbits Explained is exactly what you are looking for. On this page you will find the building blocks we will use to understand orbits. On the second webpage (see link below) you will find a summary of how the building blocks are combined to explain orbits of planets. One of the beautiful aspects of the approach used in Orbits Explained is that we don’t rely on any preexisting orbital laws or any actual observations of how planets move across the sky. In the field of Philosophy, we call an approach like ours that does not rely on observations an “a priori” approach. Instead of starting with observations of the planets in the sky, we will start with a geometrical building block that we will call the hododyne. A hododyne is fashioned from a line of fixed length that has been bent so that its two parts spin around each other. You will see that the location and speed and direction of a planet are indicated by the hododyne. The hododyne is a geometrical part of a diagram that was drawn in the 1840s by Sir William Rowan Hamilton but was somewhat hidden until the author of Orbits Explained identified it as a starting point for explaining planetary motion. Hamilton called his diagram a hodograph and in 1847 described it as a new way to explain Isaac Newton’s Law of Gravitational Attraction.
There is a companion book, Orbits Explained, to this website that presents the full stepwise development of the methods and proofs involved. Acknowledgements related to this website and the book go to Sir William Rowan Hamilton, Isaac Newton, Johannes Kepler, Richard Feynman, David L. Goodstein, Judith R. Goodstein, family, friends, and many others.
The main building block, the hododyne defined:
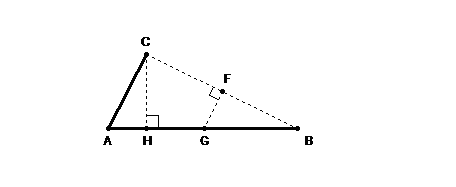
The triangle below will be our main building block for orbits. The triangle is formed by spinning the line segment AC around line segment AB where the two line segments meet at point A. Line segment CH is drawn perpendicular to line segment AB where it meets the tip of line segment AC. Line segment FG is the perpendicular bisector of line segment CB and meets line segment AB a point G. The magical property of the triangle is that as line segment AC spins, the line segments AG and HB change their lengths but remain inversely proportional to each other! This may be the first and only geometrical mathematical model to generate inverse proportions. We will call this triangle the Inverse Proportion Machine and give it a scientific name, the hododyne, – hodo implying the round or elliptical path of planets, -dyne implying force that causes movement. The easy line by line proofs for these line segments of the hododyne are given in Chapter 9 of the book Orbits Explained.
This new machine of mine
So aptly rations out a line
That when it regulates the sky
It’s called a hododyne
– David S. Marlin
These are the 3 tools that will be used to build a solid understanding of orbits:
- A proof that a planet sweeps out equal areas between it and the Sun during equal amounts of time.
2. A demonstration that in order to sweep equal areas in equal times, an inverse proportion must exist between the distance to the Sun and the speed of a planet in the direction that is perpendicular to the direction towards the Sun.
3. Our new geometric mathematical tool, the hododyne, generates line segments that are inversely proportional to each other. No calculus is involved.
These 3 tools will be used to prove Kepler’s Planetary Laws and Newton’s Inverse Square Law of Gravitational Force and Distance in “a priori” fashion without relying on astronomical observations.
You can see a free brief summary of the proofs and methods of Orbits Explained by clicking here.
A more detailed presentation of all the steps using easy math is available for those interested in the book Orbits Explained which is available for purchase on the Amazon website by clicking the link: http://amazon.com/dp/B0DP1YLH3B.
Contact information regarding Orbits Explained: dsmpublishing@orbitsexplained.com
About Orbits Explained: The proofs and the draft version of the book began to develop as a hobby and project in 2006. Years of scribbling ideas and diagrams on paper and napkins were involved. None of the methods in Orbits Explained have been reviewed by experts in the field. However, the reader will hopefully find that the stepwise logical proofs herein, using simple math, supply their own authority to the work.
-David Marlin, Los Angeles.
Orbits Explained 